مسلمة التوازي .. في عشق الهندسة أنا فت (إقليدس)

لو أنا في إيدي أعمل إستطلاع رأي يشارك فيه طلبة المرحلة الإعدادية بس نفسي أسألهم سؤال واحد .. إيه رأيك في (إقليدس Euclid)؟ .. هو يبان من أول وهلة سؤال غريب بس صدقني مع أخر المقالة دي حتحس من جواك إنك عايز تفتح كتاب الهندسة المستوية بتاع إعدادي عشان تفتكر و تقدر مدي عبقرية الرجل ده .. (إقليدس) من أهم البني أدمين اللي ربنا خلقهم في تاريخ البشر و دي مش مبالغة صدقني .. يكفي إن هو اللي حط أساس الهندسة الفراغية و الجبر و التفاضل و التكامل .. حضرتك راكب عربيتك و ماسك موبايلك و لما تيجي تشتغل بتعمل جداول بالإيكسل بسبب شغل (إقليدس) و لإن الكلام في الرياضيات و الهندسة محتاج يبقي مترتب فخليني من الأول كده أقولك هو أنا ناوي أعمل إيه في المقالة دي .. النهاردة إحنا جايين نحاول نجاوب علي كذا سؤال:

مين هو (إقليدس)؟ و إيه مشكلة مسلمة التوازي؟
إزاي (الخوارزمي) و (عمر الخيام) طلع عينيهم عشان يثبتوا مسلمة التوزازي؟
إزاي (رينيه ديكارت) بني الإحداثيات الكارتيزية و (إسحاق نيوتن) عمل التكامل علي الشغل بتاع (إقليدس)؟

خلينا نبدأ بالسؤال الأولاني .. يطلع مين الأخ (إقليدس) ده؟

بص مش حصدعك بمقدمة تاريخية ممكن تتوهك .. خليني أقولك إن (إقليدس) ده بني أدم كتب كتاب .. حاول تتخيله مجرد بني أدم له Account علي Facebook و كتب بوست .. الحقيقة هو مكنش كتاب واحد .. هم كانوا 13 كتاب جري العرف إننا نسميهم سوا علي بعض كده كتاب العناصر و فيه ناس بتحب تسميه كتاب الأصول .. عشان تستوعب بس مدي أهمية الكتاب ده أو البوست ده تخيل للحظة إن لأكثر من 2000 سنة لما حد يحب يفهم و يتعلم يعني إيه منطق بيتقاله روح يا ابني إقرأ كتاب العناصر بتاع (إقليدس) و إنت حتفهم يعني إيه منطق .. تخيل إن الكتاب ده هو ثاني أكتر كتاب إتطبع في تاريخ البني أدمين بعد الإنجيل.

بس اللي يستحق إنك تقف قدامه أكتر من الكتاب و من العلم اللي في الكتاب إنك تسقف لدماغ (إقليدس) في إنه إزاي رص أفكاره اللي هو عايز يقولها في الكتاب ده .. لإن خلينا نكون صرحاء مع نفسينا هو إن كتاب العناصر ده عامل زي ما إنت تكون في الكلية و ليكن مثلاً زي حالاتي خريج قسم ميكانيكا هندسة إسكندرية و تكون كاتب كل المحاضرات اللي إنت خدتها في كل المواد اللي إنت درستها في الخمس سنين و تقرر تحط المحاضرات دي كلها في كتاب .. هو صحيح كتاب مليان معلومات .. صحيح هو كتاب يعتبر مرجع لأي مهندس حديث تخرج .. بس لو الكتاب ده مترصش صح و بترتيب أفكار ياخد القاريء واحدة واحدة من إيده من أول ورقة لحد أخر ورقة فإنت حتكتشف إن كل اللي إنت عملته إنك عملت شوية ورق فيهم دش كتير محدش فاهم منه حاجة.

كتاب العناصر بتاع (إقليدس) هو فعلياً تجميع لكل المعلومات الهندسية اللي كانت متاحة في العصر بتاعه بس الترتيب و رصة الكتاب هي اللي مبهرة .. الكتاب بيبدأ بشوية مسلمات .. شوية أفكار بسيطة إتبني عليها الكتاب كله .. شوية أفكار تافهة إتسمت مسلمات أو Postulates إتبنت عليها الهندسة المستوية .. بمجرد ما تقرأ الكتاب حتلاقي نفسك بتقول طب ما الهندسة تافهة و حلوة أهي .. إنت مش واخد بالك إنه بيجيب رجلك بس .. بعد ما عرضلك شوية الأفكار البسيطة التافهة دي قام ساحلك في باقي الكتاب عشان يثبت كل مسلمة أو فكرة هو حطها في الأول .. كل إثبات إتحط لمسلمة بيستخدمه عشان يثبت المسلمة اللي وراها .. طوبة بتترص ورا طوبة .. إنت بتمسك الكتاب و إنت مش فاهم حاجة في الهندسة و بتسيبه و إنت مش بس عارف القواعد الأساسية فيها إنما كمان بتقدر تثبتها.

الأفكار نفسها إلي حد كبير تافهة و منطقية .. قالك إن أي نقطتين في الدنيا بيربط بينهم خط مستقيم واحد و دي كانت المسلمة الأولي .. حلو .. لو عندك قطعة مستقيمة فإنت لو مديتها من طرفيها فإنت بقي عندك خط مستقيم و دي كانت المسلمة الثانية .. طب ما سهلة أهي .. قالك عايز ترسم دايرة؟ مفيش أسهل من كده إعرف بس نقطة المركز بتاعها و نص قطرها و ببرجل من أي مكتبة بخمسة جنيه حترسمها و دي كانت المسلمة الثالثة .. قالك كل الزوايا القائمة ليها نفس القيمة اللي هي تسعين درجة و دي كانت المسلمة الرابعة .. إنت متخيل التفاهة؟ .. أربع أفكار أو مسلمات أسهل من بعض .. هي المشكلة كانت الحقيقة في المسلمة الخامسة .. هي الوحيدة اللي تحس فيها حاجة غلط .. ليه أنا بقول كده؟ .. بص لنص المسلمة و إنت تعرف:

“إذا قطع مستقيم مستقيمين و كان مجموع الزاويتين المتقابلتين عند جهة القاطع أقل من مجموع زاويتين قائمتين (يعني أقل من 180 درجة) فعند مد هذين المستقيمين من جهة الزاوتين فسوف يتقاطعان”

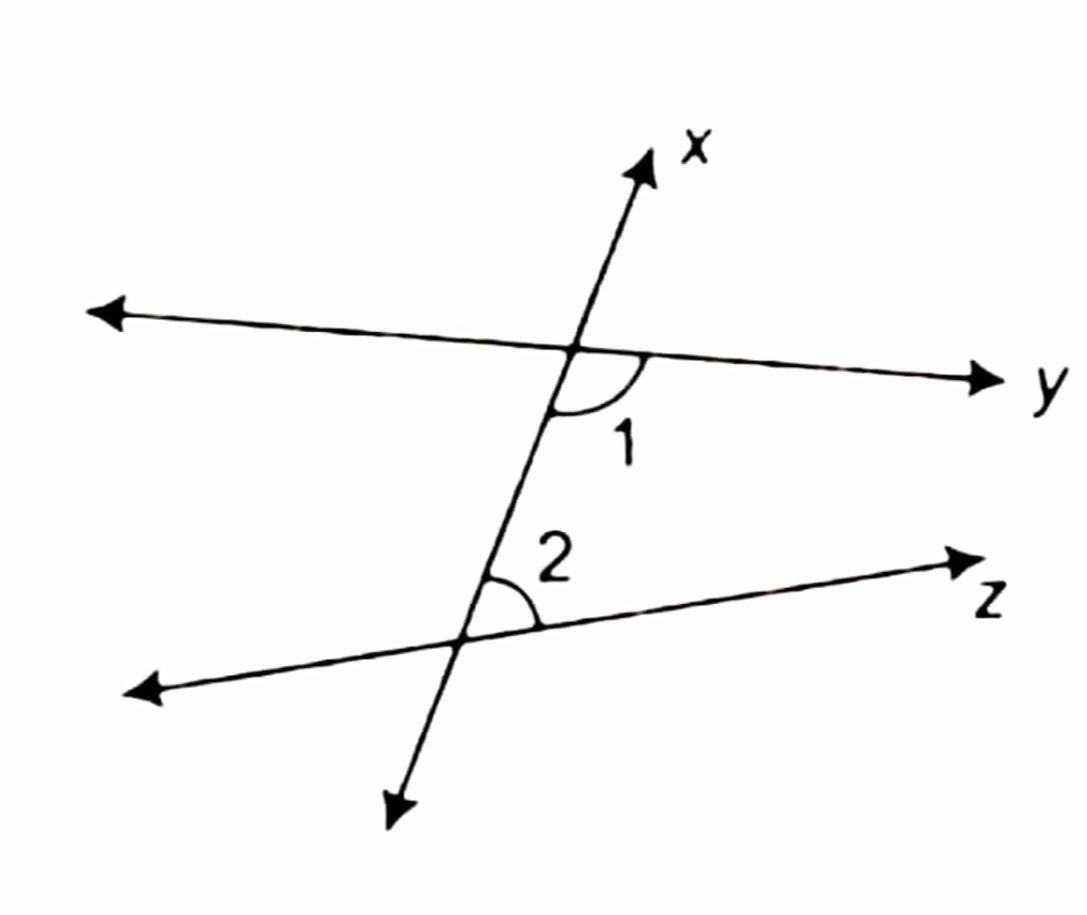
لو مش فاهم حاجة خليني أفهمهالك بالراحة .. لو عندك خط مستقيم زي X مثلاً عايش في حالة ملوش دعوة بحد فجأة و من غير أي داعي فيه خطين مستقيمين اللي هم Y و Z قطعوه .. في الحالة دي لو بصيت علي الزاويتين الداخلتين اللي هم 1 و 2 و لو لقيت مجموعهم أقل من 180 درجة فحتلاقي إن عاجلاً أم أجلاً الخطين Y و Z حيقطعوا بعض .. لما تستهدي بالله و تفكر فيها كده بهدوء حتلاقي إن الكلام بتاع (إقليدس) منطقي برده .. هو صحيح مجعلص زيادة عن اللزوم مقارنة بالمسلمات الأربعة اللي قبل كده بس الكلام منطقي .. المسلمة دي بتقول بإختصار شديد إن لو الزوايا 1 و 2 طلعوا زوايا قائمة يعني قيمهم 90 درجة فإنت كده قصاد الحالة اللي إحنا بنسميها المستقيمين المتوازيين Parallel Lines و عشان كده فيه ناس بتسمي المسلمة الخامسة أو Fifth Postulate بتاعة (إقليدس) مسلمة التوازي بس فضلت المسلمة الخامسة دي عاملة صداع مش بس في رأس (إقليدس) إنما في رأس كل الناس اللي درست الهندسة من بعده .. مشكلة مسلمة التوازي إنك تحس إن مينفعش يتقال عليها مسلمة .. دي الفكرة الوحيدة اللي (إقليدس) معرفش يثبتها في كتاب العناصر بس إستخدمها لإثبات المسلمات الثانية و هي دي المشكلة .. ناس كتير كانت شايفة إن المسلمة الخامسة دي هي نظرية محتاجة إثبات مش مسلمة.

مسلمة التوازي بتاعة (إقليدس) بتقول إن لو مستقيم X قطعه مستقيمين Y و Z و كان مجموع الزاويتين الداخلتين اللي هم 1 و 2 أقل من 180 درجة ففي مرحلة ما حتلاقي إن المستقيمين Y و Z حيقطعوا بعض .. ده معناه إن لو زوايا 1 و 2 كانوا زاويتين قائتمين يعني قيمهم 90 درجة فالمستقيمين Y و Z حيبقوا مستقيمين متوازيين Parallel Lines.

هنا يجي دور السؤال الثاني .. إيه بالضبط اللي عمله (عمر الخيام) و (الخوارزمي)؟

إنت مش متخيل إزاي الحضارة الإسلامية أنقذت العالم .. أنا مش عايز أخش في الجدل بتاع الفتوحات الإسلامية لإن ده مش مجالنا النهاردة .. اللي عايزين نتكلم عنه هو إن إزاي بعد إنهيار الدولة الرومانية و في الوقت اللي الدولة البيزنطية مكنتش عارفه تصلب طولها كانت الدولة الإسلامية سواء الأموية و وراها العباسية كانت ماشية زي القطر في سكة إنها تجيب الكتب اللي كتبها العلماء الإغريق و يترجموها للغة العربية و مش بس كده .. يحطوا التاتش بتاعتهم فيها.

فيه مصطلح إنت ممكن تكون سمعته أو حتسمعه و هو Islamic Golden Age أو العصر الذهبي للإسلام و دي بتتقال علي فترة حكم العباسيين اللي كان الفرق في التطور العلمي بينهم و بين أوروبا مثلاً زي الفرق بين فرقة بايرن ميونيخ و بلدية المحلة كده .. في فترة العصر الذهبي للإسلام ده حصل شوية نطات في الرياضيات إنت شخصياً عايش علي حسها دلوقتي .. في الفترة دي إتحط الأساس اللي إتبني عليه علم الجبر Algebra .. حساب المثلثات Trigonometry بقي فرع من فروع الرياضيات مش مجرد سحر و شعوذة .. بس العلوم زيها زي الديانات حتلاقي ناس مقتنعة إن فيه أفكار معينة بتتصنف علي إنها شرك بالله و من ضمن الأفكار في علم الرياضيات اللي كان بيتبصلها علي إنها كفر كانت الأعداد النسبية Rational Numbers اللي هي الكسور.

(عمر الخيام) لو إنت مثقف فإنت عارفه بسبب الرباعيات بتاعته في الشعر .. لو إنتي بنت فإنتي غالباً عارفاه من كتاب قواعد العشق الأربعين .. بس لو إنت دحيح حتبقي عارف إنه كان الأنتيم بتاع (حسن الصباح) مؤسس الحشاشين .. بس النهاردة حنحكي إزاي إن الرجل ده شقلب دماغ مدرسين الرياضيات في عصره لما قالهم هو ليه لا نحط الأرقام الكسرية علي خط الأعداد جنب أخواتها الأعداد الصحيحة Irrational Numbers؟ .. الفكرة إن الأخ (إقليدس) كان بيحب الحنتفة حبتين تلاتة .. هو كان مقتنع أن أي حاجة في الدنيا تقدر تقيسها و عشان كده إنت لو جيت قلتلي أنا عايز لوح خشب طوله أربعة متر فبسيطة حيبقي عندي حبل طوله متر و حنفضل نقيس متر وراه متر وراه متر لحد ما نعرف الأربعة متر دول أخرهم فين و حقطعلك لوح الخشب الكبير اللي عندي في المحل عشان تاخد الأربعة متر اللي إنت عايزهم .. لكن لو جيت قلتلي أنا عايز لوح خشب طوله 2.43 متر .. حقيسلك أنا ال 0.43 متر دول إزاي؟

ده خلي (إقليدس) يقول إن بما إني مش حعرف أقيس أي حاجة بالكسور فالمنطقي إن الأعداد الصحيحة و الأعداد النسبية دول زي الأهلاوية و الزملكاوية مستحيل تلاقيهم مولفين علي بعض .. علي الناحية الثانية (عمر الخيام) كان بيسأل سؤال منطقي الصراحة .. هو إنت مش عارف إن قيمة ط أو باي اللي هي 3.14 أكبر من الواحد الصحيح؟ .. أكيد إنت عارف المعلومة دي يعني .. إذن أكيد فيه علاقة بين ال ط و بين الواحد الصحيح .. إذن ليه لا نجيب خط الأعداد و زي ما بنرص عليه الأعداد الصحيحة نقدر نحشر بينهم الأعداد الكسرية؟

(عمر الخيام) كان هو صاحب فكرة ليه لا نحط الأعداد النسبية Rational Numbers علي نفس خط الأعداد جنب أخواتها الأعداد الصحيحة Irrational Numbers و دي الفكرة اللي لو كانت إتقالت زمان وقت الإغريق كانوا قالوا عليها بدعة من بدع الشيطان.

الفكرة بتاعة (عمر الخيام) خدها واحد ثاني اسمه (محمد بن موسي الخوارزمي) و طلع بيها علي الرابع .. (الخوارزمي) ده لمن لا يعلم يعني هو السبب في إن حضرتك بتكتب الأرقام بالعربي بالشكل ده لإنه كان شايف إن الأرقام الهندية مناسبة جداً و هو اللي دخلها عشان تبقي شكل الأرقام العربية .. (الخوارزمي) هو اللي قال إن فيه حاجة اسمها علم الجبر Algebra .. المهم .. عشان تفهم اللي (الخوارزمي) كان عايز يعمله بص علي المعادلة التربيعية دي: X^2+10X=39 .. لو إديت المعادلة دي لأي طالب في إعدادي أو ثانوي و قلتله حلها فكل اللي حيعمله إنه حيروح للطريقة دي: X=(b*SQR(b^2-4ac))/2a .. بس (الخوارزمي) محلهاش كده .. (الخوارزمي) حلها بطريقة تجيب صداع حرفياً و لإني عايز أصدعك معايا فإمشي معايا في الخطوات اللي حتلاقيها في الصور.

بما إننا مش عارفين قيمة X فخلينا نرسمها علي إنها مسافة ثابتة احنا حنفرضها دلوقتي بإنها مثلاً يعني 3 سنتيمتر .. بما إن المعادلة تربيعية فإحنا حنرسم مربع ضلعه طول X اللي إحنا فارضينه و مش عارفين قيمته .. بعد كده المعادلة فيها 10X .. حلو .. إحنا بقي حنقسم 10X دي علي حتتين .. تعالي إنت علي الضلع اللي فوق من المربع بتاعك مده بمسافة 5 سنتيميتر .. كرر نفس الخطوة مع الضلع اللي تحت .. كده إنت بقي عندك الحتة المظللة دي .. الحتة المظللة دي بتعبر عن X^2+5X+5X اللي هي X^2+10X .. لو كملت المربع بتاعك حتلاقي ان فيه حتة مش مظللة بس إحنا الحمد لله عارفين قيمتها اللي هي 5 مضروبة في 5 اللي هي 25.

ده معناه إن الحتة المظللة الأولانية اللي هي قلنا إنها بتساوي X^+10X و المعادلة بتاعتنا قالت إن ده بيساوي 39 .. فلو عايز تعرف مساحة المربع بتاعك كلها فإنت حتجمع ال39 دول مع ال25 اللي كانوا فاضلين عشان المربع يكمل .. جميل .. إذن مساحة المربع كلها 64.

بس إحنا عارفين إن مساحة المربع هي الطول في العرض .. و عارفين إن المربع بتاعنا طول ضلعه هو X+5 .. فلو أنا ضربت X+5 في نفسها يعني (X+5)^2 فهي حتساوي 64 اللي هي قيمة مساحة المربع بتاعي.

شوف يا أخي طلعت X=3 زي ما فرضت في الأول عشان بس تعرف إن فيا شيء لله.

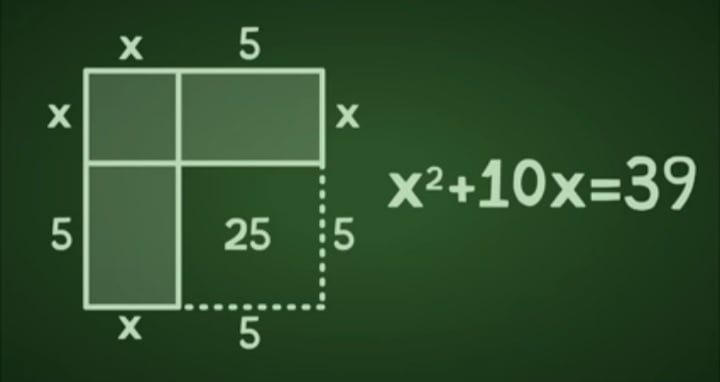
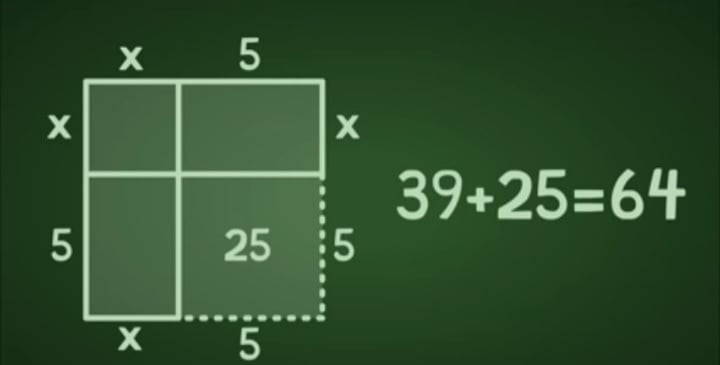
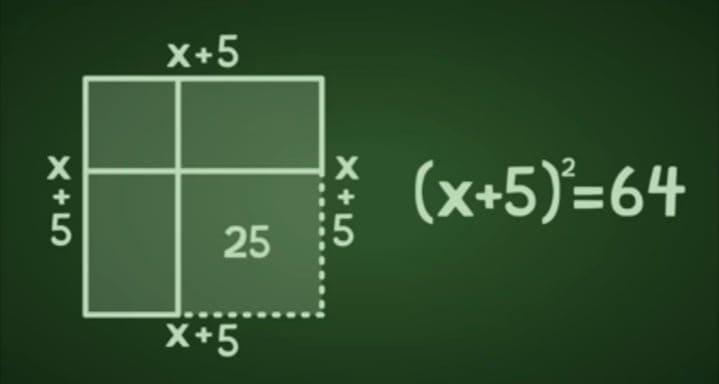
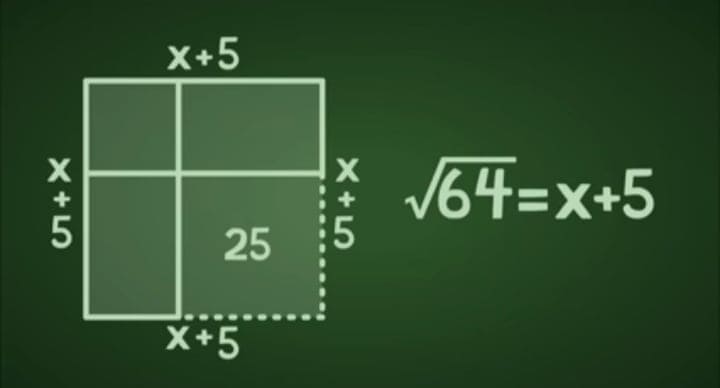
أنا ليه سحلتك معايا في الخطوات دي كلها و خليتك تحل معادلة تربيعية مش بالجبر إنما بالهندسة المستوية؟ .. عشان بس أوريك قد إيه دماغ (الخوارزمي) كانت متكلفة .. تخيل دماغ الرجل اللي فكر في الحل ده منظمة إزاي .. و لك أن تتخيل إن (الخوارزمي) و (عمر الخيام) قضوا سنين من عمرهم بيحاولوا يثبتوا مسلمة التوازي بتاعة (إقليدس) .. (عمر الخيام) ساب الشعر و ساب قواعد العشق الأربعين و كتب كتاب كامل عشان يحاول يفسر و يلاقي إثبات منطقي لمسلمة التوازي ل(إقليدس) .. كل علماء الرياضيات المسلمين حاولوا يلاقوا تفسير منطقي للبتاعة دي و محدش عارف يفسرها لحد ما جت الحملات الصليبية.

برده أنا مش عايز أدخلك في تاريخ الحملات الصليبية و إزاي بدأت بس خليني أقولك إن مش كل الأوروبيين كانوا راضيين عن اللي بيحصل و من ضمنهم كان قسيس إنجليزي اسمه (أديلار Adelard) إتولد في حتة اسمها باث Bath و عشان كده حتلاقي اسمه في المراجع (أديلار الباثي) .. (أديلار) بدأ يزور الأراضي الإسلامية اللي الصليبيين سيطروا عليها و من ضمن الحاجات اللي بهرته كانت المكتبات .. الرجل ده لما لقي الكتب بتاعة سواء العلماء الإغريق أو العرب لقي نفسه بيقول وه .. في الوقت اللي كتير من القساوسة الكاثوليك كلوا الشهد من الترويج لفكرة إن لو إنت بني أدم كاثوليكي فإنت حتخش الجنة حدف لو إنت قتلت مسلم في سبيل إستعادة القدس ف(أديلارد) قضي سنين بيترجم الكتب اللي كتبها العلماء العرب للغة اللاتينية .. و من ضمن الكتب دي كان كتاب العناصر بتاع (إقليدس).

لمدة 600 سنة لو أي حد عايش في أوروبا حب يفهم يعني إيه هندسة مستوية بيتقاله روح إقرأ ترجمة القس (أديلار) لكتاب العناصر بتاع (إقليدس) اللي هو أساساً ترجمه من الكتب العربية .. لأكتر من 600 سنة و الترجمة اللاتينية لكتاب العناصر موجودة في مكتبة الفاتيكان للي عايز يقراه لحد ما في مرة (نابليون بونابرت) سرق الكتاب من جوه مكتبة الفاتيكان ودي قصة تانية ممكن نحكيها في وقت تاني.

نيجي بقي للسؤال اللي وراه .. إيه اللي عمله (ديكارت) و (نيوتن)؟

زي ما قلتلك لأكتر من 600 سنة و ترجمة كتاب العناصر اللي كتبها (أديلار) كانت هي المرجع الوحيد لأي حد عايز يفهم يعني إيه هندسة مستوية في أوروبا بس الحقيقة إن اللي كانوا بيعرفوا يقروا و يكتبوا في أوروبا وقتها يتعدوا علي الصوابع و أكيد يعني هم مش حيقضوا يوم من عمرهم عشان يقروا كتاب عن الهندسة المستوية .. لحد ما جت سنة 1450 .. في السنة دي الأوروبيين إخترعوا مكنة الطباعة .. جري الشريط أقل من 100 سنة و كان كتاب العناصر هو ثاني أكتر كتاب إتطبع في أوروبا بعد الإنجيل .. كتاب العناصر بقي عامل زي أغنية بنت الجيران .. إنت ممكن متكونش بتحب تسمع أغاني مهرجانات و شايفها إسفاف بس إنت لازم تكون سمعت الأغنية دي .. ده حيوديني إني أتكلم عن ثالث شخصية في قصة مسلمة التوازي .. بعد ما إتكلمنا عن (إقليدس) و (الخوارزمي) و (عمر الخيام) جه معاد اننا نتعرف علي (رينيه ديكارت Rene Descartes).

(ديكارت) كان شاب فرنساوي مش عايز وجع دماغ و مش بيحب الزن لإن أبوه كان زنان .. أبوه كان عايزه يطلع محامي و لإن (ديكارت) مكنش بيحب الزن فكان أسهل حاجة يعملها إنه يقول حاضر .. عايزيني أخش مدرسة للجيزويت .. حاضر .. عايزيني أخد شهادة في المحاماة .. حاضر .. بمجرد ما خد الشهادة في إيده تقدر تقول قال لأبوه عايز حاجة تاني يا عم الحاج؟ .. سلام أنا بقي .. (ديكارت) طلع كل الكبت اللي كان جواه لسنين مرة واحدة .. هو جاب صدمة لأهله لما عرفوا إنه ساب فرنسا و سافر هولندا عشان يشارك في الحرب الهولندية الإسبانية .. هو كان متوقع إنه حيعيش دور (إنديانا جونز) بس لقي نفسه أول ما راح هولندا سألوه انت بتعرف تقرأ و تكتب؟ .. قالهم اه ده أنا لهلوبة .. قالوله حلو .. حطوه في سلاح المهندسين و حطوا قدامه كتاب العناصر بتاع (إقليدس) و قالوله إقرأ ده و أفهمه عشان حتبني كباري بعدد شعر راسك طول ما إنت هنا .. يدوبك كام سنة و (ديكارت) قال لنفسه أصل أنا مش هربان من أبويا عشان كان كل شوية يقولي ذاكر أقوم أجي هنا عشان يتقالي ذاكر تاني .. (ديكارت) خد بعضه و طلع علي الإمبراطورية الرومانية المقدسة اللي إنت عارفها باسم ألمانيا .. يدوبك كام يوم في ألمانيا و لقي نفسه محبوس .. و هو في حبسته متفهمش إيه اللي حصل بس طلع منها بالفكرتين اللي قلبوا الدنيا.

الفكرة الأولانية الإحداثيات الكارتيزية Cartesian Coordinates و دي تقدر تقول إنها الUpgrade بتاع فكرة (الخوارزمي) اللي سحلتك فيها من شوية و دي إنك تحول أي معادلة جبرية لمسألة هندسة مستوية و العكس إنك تجيب أي مسألة هندسة مستوية تقلبها مسألة جبر و الفكرة دي إتبنت علي الشغل بتاع (إقليدس) .. الفكرة الثانية هي الإثبات العلمي و دي معناها إن مفيش حاجة اسمها أصل هي كده .. مينفعش يتقالك أصل اللي قبيلنا قالوا كده أو إن هذا ما وجدنا عليه أباؤنا و أجدادنا .. اللي (ديكارت) كان بيقوله إن أي حاجة إتكتبت في الكتب مينفعش الناس تصدقها و تؤمن بيها إلا لما تخضع للتجارب العلمية و هي دي المشكلة .. إفرض لو الحاجة اللي أنا عايز أتكلم فيها مينفعش أعملها تجربة .. إفرض يا اخي إني عايز أعمل Modeling أو محاكاة أو نموذج رياضي من شوية معادلات رياضية و ده اللي حيودينا للكلام عن الشخصية الرابعة معانا .. (إسحاق نيوتين Isaac Newton).

(إسحاق نيوتين) كان عارف إن عنده مشكلة عويصة .. هو كان ساحل دماغة في محاولة إنه يفهم الجاذبية .. إزاي الشمس جاذبيتها بتخلي الأرض و باقي الكواكب تلف حوليها .. لو مشينا ورا كلام (ديكارت) فإحنا فعلياً مش حنعرف نعمل تجربة علمية نثبت بيها الجاذبية الأرضية .. إنت أساساً عشان تدرس الجاذبية بتاعة الشمس يبقي إنت حتتكلم عن الحركة في منحنيات .. منحني يعني Curve .. يعني حتلاقي نفسك لبست في الحيط .. ليه؟ .. عشان لحد وقت (نيوتن) مكنش فيه حد عارف إزاي يحسب المساحة تحت أي Curve أو منحني .. الموضوع كان خلي بتوع الرياضيات يجيلهم حالة يأس لدرجة إن في اللغة الانجليزية بقي فيه مصطلح كده اسمه Squaring the Circle و ده بيتقال لما تسحل نفسك في مشكلة ملهاش حل.

دلوقتي إنت عشان تدرس الجاذبية لازم تعمل Modeling لحركة الأرض حول الشمس .. يعني تعمل نموذج رياضي بشوية معادلات رياضية تشرح بيها إزاي الأرض بتلف حول الشمس .. ده معناه إن لازم (نيوتن) قبل ما يشد خط في شرح الجاذبية إنه يجيب شنطة العدة اللي هو حيشتغل بيها و شنطة العدة دي كانت إنه يلاقي طريقة يحسب بيها مساحة المنحنيات .. بمعني أخر إنه يؤسس الحاجة اللي إنت عارفها باسم التفاضل و التكامل Calculus .. أيوه .. إحنا دلوقتي حنعرف هو يعني إيه تكامل؟

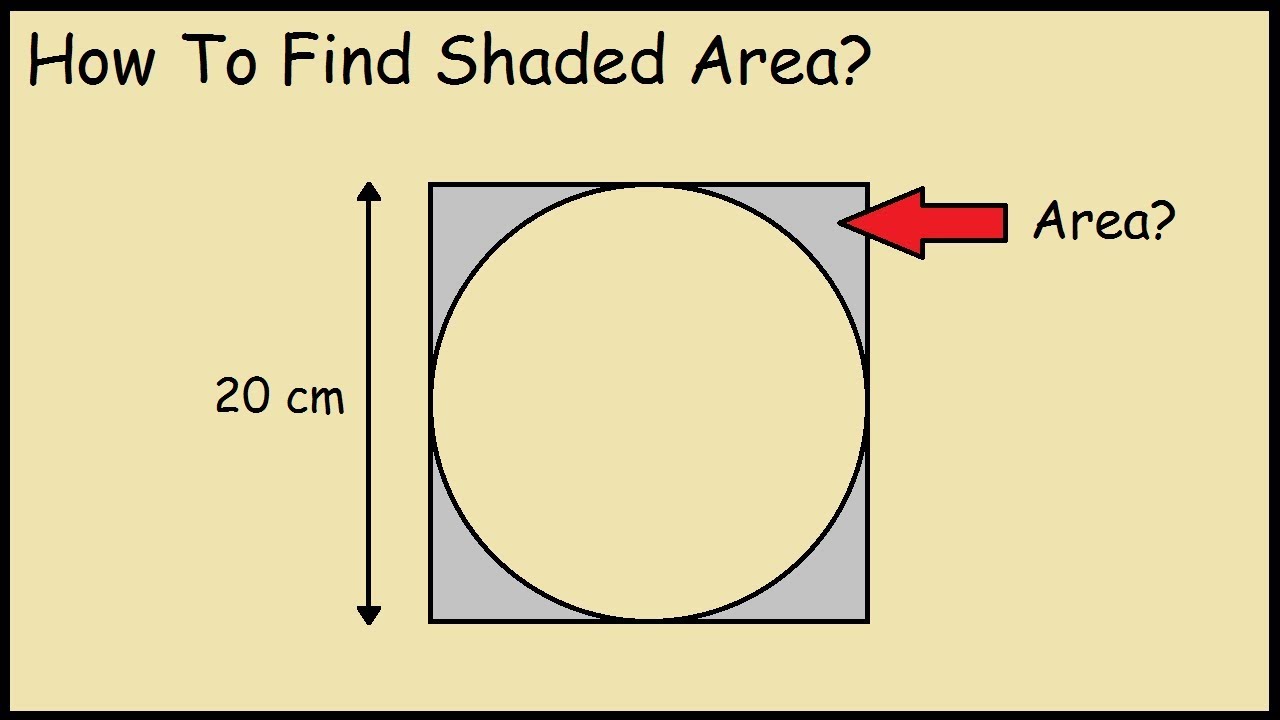
فضلت مشكلة المنحنيات إن الناس مش عارفة تحسب مساحتها .. يعني لو أنا رسمت مربع جواه دايرة زي اللي قدامك دي .. هل فيه معادلة تحسب مساحة الحتة المظللة دي؟ .. هل فيه معادلة تحسب مساحة منحني؟

التكامل ده عبارة عن أكلة جديدة عملها ناس بتعرف تخش المطبخ وإتفرجوا كتير علي حلقات برنامج ماستر شيف .. بمعني أخر .. التكامل عمله ناس قرت كلام (إقليدس) وفاهماه كويس وفي نفس الوقت عايزة تمشي علي الكلام اللي حطه (رينيه ديكارت Rene Descartes) .. التكامل هو بتاعة كده عملناها عشان نحسب المساحة اللي تحت أي منحني .. ليه عملناها؟ .. قالك عشان إحنا كنا عايزين ندرس الجاذبية فإحنا حنتعامل مع كيرفات Curves بالهبل علي أساس إن الأرض مثلاً بتدور حول الشمس في مسار بيضاوي يعني Curve برده فأكيد يعني حنحتاج في مرحلة ما إننا نحسب المساحة اللي تحت المنحني .. وعشان منزعلش الأخ (ديكارت) اللي قالك إنت لازم تختبر أي حاجة تطلع من بقك فإحنا لازم نبقي عارفين إننا عشان نعمل تجربة معملية عشان نثبت الجاذبية فإحنا مش حنعرف .. أصلك حتجيب حاجة زي الأرض منين تقولها لفي حول حاجة زي الشمس عشان الأخ (ديكارت) ميتقمصش .. إذن إنت محتاج تعمل نموذج رياضي للجاذبية .. بمعني إنك تعمل شوية معادلات توصف وتشرح بيها تطلع إيه الجاذبية دي؟

عشان تفهم يعني تكامل فإنت محتاج تستوعب يعني إيه Integral .. كلمة Integral لو دخلت علي أي قاموس تعرف معناها بالعربي مش حتلاقي فبلاش تتعب نفسك .. خليني هنا أقولك يطلع إيه الIntegral ده من الخطوات اللي جاية:

الخطوة الأولي لو عندي منحني أو Curve زي اللي عندك في الصورة ده وطالبة معايا أحسب المساحة اللي تحت الCurve ده قد إيه؟ .. قالك تعالي إنت إرسم مستطيلات زي ما إنت شايف كده بحيث المستطيلات دي كلها القاعدة بتاعتها كلهم قد بعض .. المستطيلات دي يطلع عددها زي ما إنت عايز مش مشكلة .. المهم إن المستطيل مساحتة الطول في العرض زي ما إنت عارف .. أهو إحنا بقي عايزين العرض بتاع المستطيلات دي كلها يبقي موحد.

الخطوة الثانية .. تعالي علي أول مستطيل رسمته وتعالي علي الركن اليمين فوق بتاعه إطلع بخط رأسي وإمشي بالعرض للشمال لحد ما تلمس أول المنحني .. كرر نفس الخطوة مع كل المستطيلات اللي بعده.

الخطوة الثالثة .. واضح كده إننا رسمنا شوية مستطيلات شكلها شبه شوية شكل المنحني بتاعنا بس المستطيلات بتاعتنا مش دقيقة أوي .. واضح زي ما إنت شايف إن فيه حتت من المستطيلات بتاعتنا طالعة بره المنحني .. لحد هنا (نيوتن) مقالش حاجة جديدة عن (إقليدس) لحد ما (نيوتن) حط التاتش بتاعته في الخطوة الجاية.

الخطوة الرابعة .. جه (نيوتن) قالك طب ما تصغر مساحة المستطيلات بتاعتك .. ليه لا تخليها مستطيلات رفيعة وكتيرة .. ليه لا تخليها عدد لا نهائي من المستطيلات الرفيعة أوي .. كل ما تعمل ده تلاقي مساحة المستطيلات بتاعتك بقت قد المساحة اللي تحت المنحني.

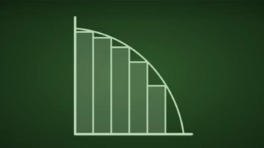
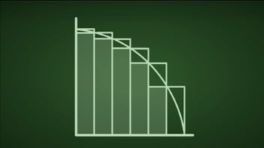
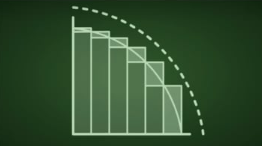
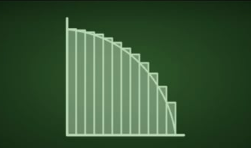
فكرة التكامل زي ما قلتلك هي مجرد إنك تعرف فيه كام مستطيل رفيع صغنون إنت محتاجه تحت المنحني عشان لما في الأخر تجمع مساحة المستطيلات دي كلها تطلع قد المساحة اللي تحت المنحني .. فكرة تافهة هي مجرد Upgrade للكلام بتاع (إقليدس) بس الفكرة لما إتضربت في الخلاط مع فكرة الإحداثيات الكرتيزية بتاعة (ديكارت) لما إتحطوا في كتاب الأصول الرياضية للفلسفة الطبيعية وده الإسم العربي الطويل أوفر لكلمة The Principia وده كان عنوان الكتاب اللي كتبه (نيوتن) فالكتاب ده نقل البشر سنين ضوئية لقدام .. الكتاب ده خلاك إنت كمهندس أو واحد بتحب الرياضيات تبقي عارف إنك تقدر تعمل نموذج رياضي أو Mathematical Model لأي حاجة في الدنيا .. عرفنا نعمل نموذج رياضي لحركة الكواكب حول الشمس .. عرفنا نعمل نموذج رياضي لحركة الأليكترونات حول النواة .. عرفنا سر الطاقة النووية .. بس فضل كل ده مربوط بكلام (إقليدس) .. لحد دلوقتي العلم مجابش حاجة جديدة أوي يعني .. كلها يا إما تطوير أو إجتهاد جديد لفهم كلام (إقليدس) وخصوصاً مسلمة التوازي.

فضل السؤال اللي عامل هسهس للناس بتوع الرياضيات هو إيه إحتمالات إن (أقليدس) يبقي غلطان .. أو بلاش غلطان يا سيدي عشان دي كلمة صعبة أوي .. حاول تتخيل إنك فضلت طول عمرك تعرف اللي بيحصل ماتشات الكورة من الراديو .. إنت عمرك ما قعدت قدام تليفيزيون وإتفرجت علي ماتش .. إنت دايماً بتسمع الماتش في الراديو .. صحيح إنت عارف النتايج وعارف مين أحسن اللاعيية في كل فرقة بس بمجرد ما أديك الفرصة إنك تتفرج بعنيك علي ماتش كورة فإنت منظورك عنها حيختلف خالص .. محدش قال إنك عشان كنت بتسمع التعليق علي الماتشات في الراديو إنك مش فاهم يعني إيه كرة قدم .. بس إنك تتفرج عليها ده موضوع تاني .. إرجع تاني لمسلمة التوازي .. دلوقتي (أقليدس) قال لو مستقيمين قطعوا مستقيم وكان مجموع الزاويتين الداخلتين قد بعض ومجموعهم 180 درجة فالمستقيمين دول بيتقال عليهم مستقيمين متوازيين أو Parallel Lines .. حلو .. لو ده كلام (أقليدس) فإيه هي الإحتمالات التانية؟ .. إيه إحتمالات إنه يبقي غلطان؟

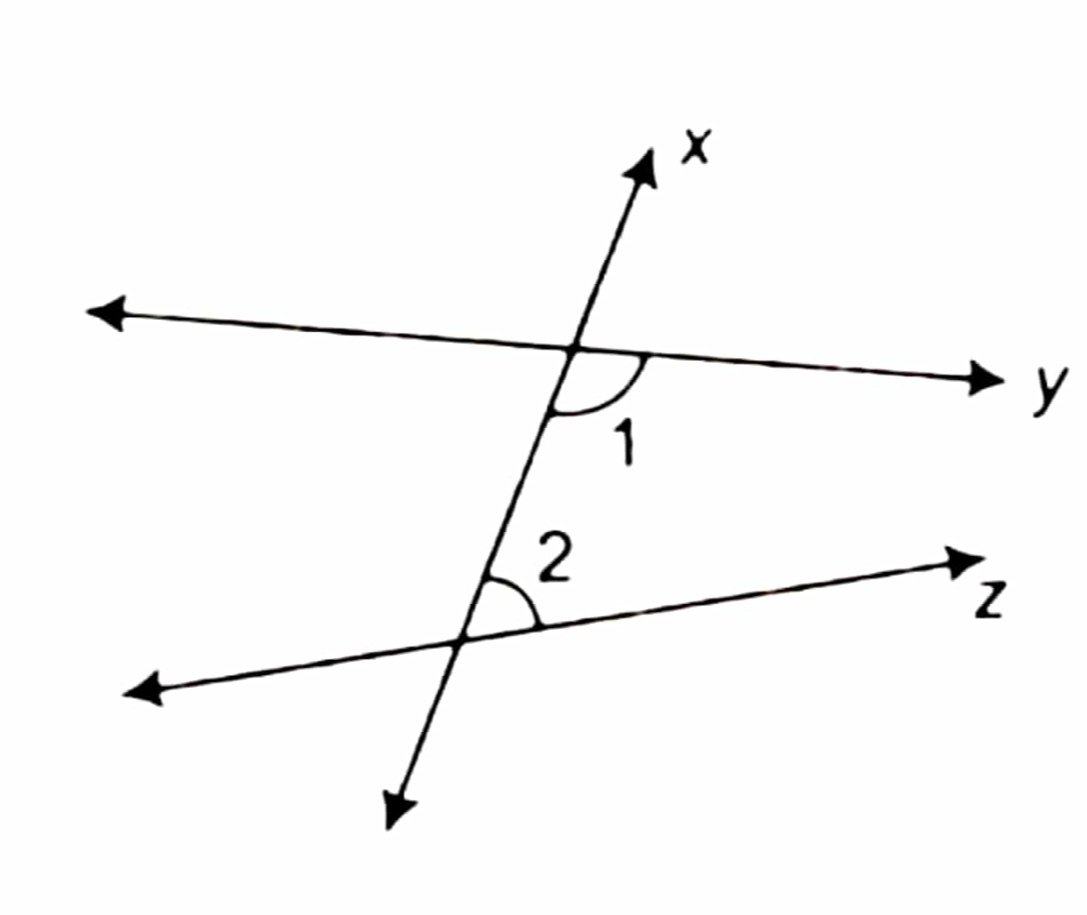
مسلمة التوازي ل(أقليدس) إن لو مستقيمين قطعوا مستقيم وكانت زاوية 1 و 2 مجموعهم 180 درجة فده ملوش إلا معني واحد وهو إن المستقيمين Y و Z متوازيين .. بس إيه إحتمالات إن (إقليدس) يبقي مش حقول غلطان بس مش شايف الصورة كاملة؟ .. ممكن مستقيمين Y و Z يكونوا حيتقاطعوا قدام أو حيبعدوا عن بعض قدام برده.

الإحتمال الأول .. المستقيمين مش متوازيين ولا حاجة .. دول حيبعدوا عن بعض:

عايزك تتتعرف علي إتنين علماء واحد إسمه (يانوش بولياي Janos Bolyai) والثاني إسمه (نيكولاي لوباتشيفسكي Nikolai Lobachevsky) والإتنين قالوا حاجة بسيطة جداً .. هي الأرض مش كروية؟ اه .. يعني الأرض مش مسطحة؟ لا مش مسطحة .. حلو يبقي الورقة اللي إنت حترسم عليها المستقيمين مش ورقة مفرودة زي ورقة الكراسة .. دي ورقة واخدة شكل منحني كأنها جزء من دايرة .. ولإن المستقيمين مرسومين علي ورقة كيرفي فأكيد هم كمان حيطلعوا مستقيمين كيرفي .. اللي هو حاجة (ياسمين الخطيب) في نفسها كده.

دي لوحة رسمها فنان أمريكاني إسمه (إم سي إيشر M.C. Escher) وزي ما إنت شايف هو متأثر أوي بشكل (يانوش بولياي Janos Bolyai) و(نيكولاي لوباتشيفسكي Nikolai Lobachevsky) .. رغم إنهم بتوع رياضيات إلا إنه كفنان عجبته فكرة إنك ترسم علي مستوي مش مسطح إنما كيرفي.

الإحتمال الثاني .. المستقيمين مش متوازيين يا جدعان .. دول متقاطعين:

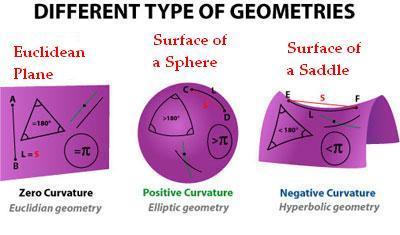
دلوقتي أنا عايزك تتعرف علي واحد ثالث إسمه (بيرنارد ريمان Bernard Riemann) .. الرجل ده بص للناس وسألها سؤال صادم الحقيقة .. أنتوا تاعبين نفسكوا ليه ما تبصوا لخطوط الطول .. إفتح أي خريطة في أي أطلس يعجبك وبص علي خريطة العالم وبص علي خطوط الطول حتلاقيها خطوط متوازية .. ليه؟ .. عشان إنت راسم الكرة الأرضية علي ورقة كراسة مفرودة .. بص للكرة الأرضية بشكلها الحقيقي اللي هو كورة وحتلاقي إن خطوط الطول كلها متقاطعة في نقطين اللي هم القطب الشمالي والجنوبي .. اللي عمله (بيرنارد ريمان) إنه كمل علي شغل (يانوس بولياي) و(نيكولاي لوباتشيفسكي) .. طول ما إنت بتتكلم عن ورقة مش مسطحة .. طول ما إنت بتتكلم عن مستوي كيرفي مش مفرود فمفيش حاجة إسمها خط مستقيم .. كلام (أقليدس) زي الفل لو إنت باصص للكرة الأرضية من منظور الأطلس .. بص للكرة الأرضية علي حقيقتها وحتلاقي حقيقة تانية خالص .. الدنيا كلها كيرفات .. الدنيا كلها (ياسمين الخطيب) .. اللي عمله (بيرنارد ريمان) إنه بدأ يحط أساسات فرع جديد في الهندسة إسمه Hyperbolic Geometry واللي أرجع وأقولك إني بسميها هندسة (ياسمين الخطيب).

زي ما لو إنت إتفرجت علي أي صورة ل(ياسمين الخطيب) علي أنستجرام وحسيتها إنها كيرفي أوفر فبرده في Hyperbolic Geometry كل حاجة أوفر .. في الهندسة المستوية بتاعة (أقليدس) إنت إتقالك إن مجموع قياسات الزوايا الداخلة للمثلث هي 180 درجة .. إرسم نفس المثلث علي ورقة كيرفي وحتلاقي إن مجموع قياسات الزوايا الداخلة للمثلث أكبر من 180 درجة .. نفس الكلام علي المربع مثلاً .. إنت إتقالك إن مجموع قياسات زوايا المربع الداخلية 360 درجة ده لو إنت راسمه علي ورقة كراسة .. إرسم نفس المربع علي كيرف وحتلاقي إن مجموع قياسات زواياه أكبر من 360 درجة .. الكلام اللي قاله (بيرنارد ريمان) إنت شفته بعنيك في حصة الفيزياء لما شفت المجال المغناطيسي .. في حصة المجال المغناطيسي في الفيزياء إتقالك إن فيه واحد إسمه (كارل فريدريش جاوس Carl Friedrich Gauss) هو اللي حط النموذج الرياضي أو Mathematical Model بتاع المجال المغناطيسي .. أهو (جاوس) يبقي استاذ (بيرنارد ريمان) .. ولفي بينا يا دنيا.

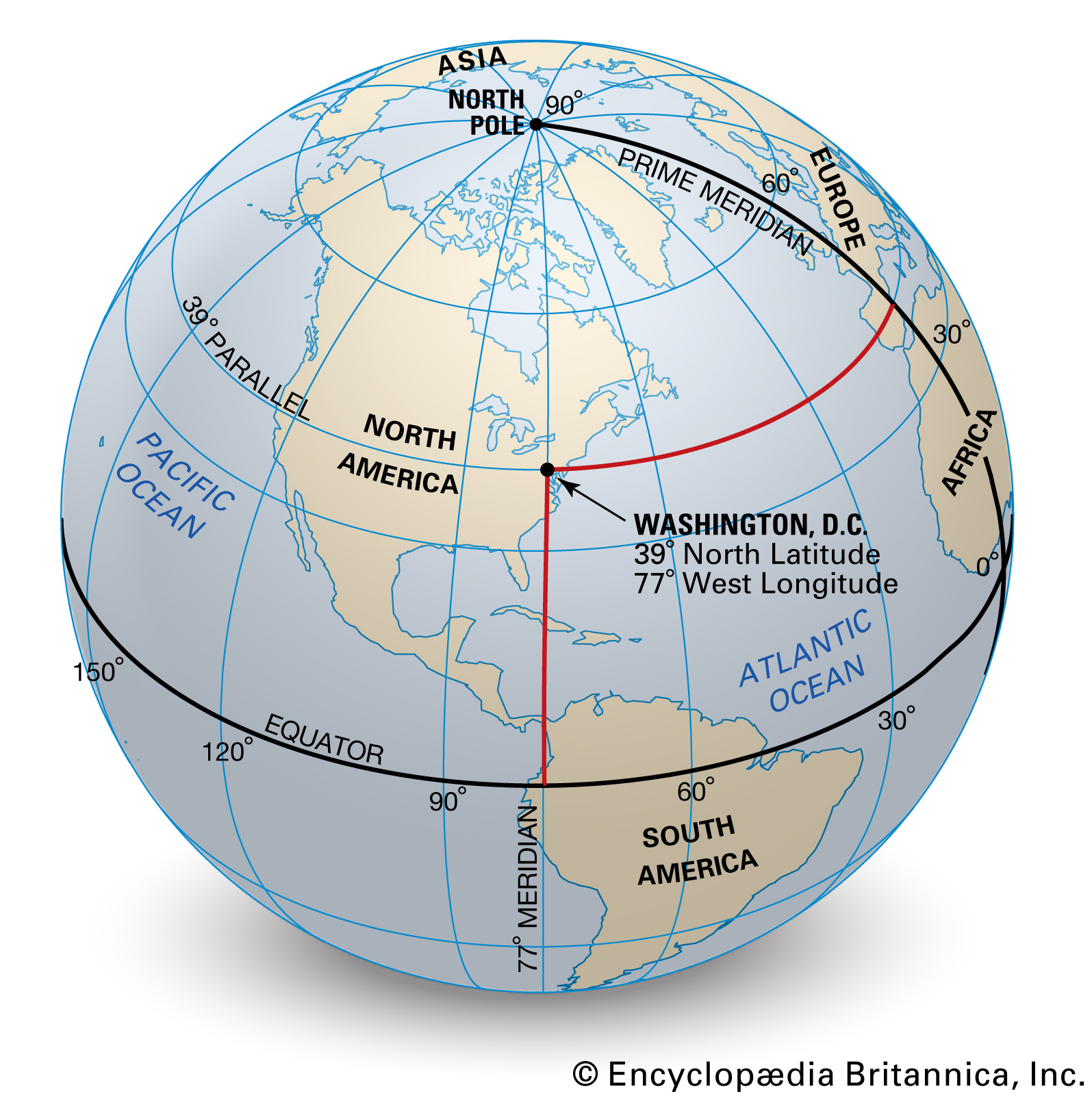
بص علي خطوط الطول بتاعة الكرة الأرضية .. أهي خطوط متوازية لو إنت رسمتها علي ورقة مستوية .. إرسمها علي كرة أرضية حتلاقيها خطوط كلها متقاطعة في نقطتين اللي هم القطب الشمالي والجنوبي.

فكرة Hyperbolic Geometry بتاعة (بيرنارد ريمان Bernard Riemann) هي إنك لو رسمت مثلث علي ورقة مستوية فصحيح مجموع زواياه الداخلة حتبقي 180 درجة بس إرسم نفس المثلث علي بلونة مثلاً يعني سطح مش مستوي وحتلاقي إن زوايا المثلث بقت أكبر من 180 درجة.

النظرية النسبية .. هي هي كلام (إقليدس) بس بالفصحي:

مفيش حد درس في كلية علوم ومسمعش عن التجربة دي .. The Michelson-Morley Experiment .. دي تجربة علمية عملها إتنين واحد إسمه (ألبيرت مكيلسين Albert Michelson) والثاني إسمه (إيدوارد مورلي Edward Morley) .. الهدف من التجربة دي كان إنهم يدرسوا حاجة إسمها الأثير Aether .. لا مش بتاع فيلم Thor: The Dark World .. الفكرة إن في الوقت ده العلم كان بيحاول يجاوب علي سؤال سخيف ودمه تقيل .. هو الضوء بيتحرك إزاي؟ .. إحنا عارفين الصوت بيتحرك إزاي .. إحنا عارفين إن الصوت هو موجة أو Wave ولإنه موجة فهو بيتحرك وسط حاجة زي الهواء أو المياه .. لكن الضوء إيه حكايته؟ .. الضوء بيتحرك في أي حاجة .. لا فارق معاه إن يبقي فيه هواء أو فراغ .. طب هو بيتحرك في إيه؟

تجربة (ألبيرت مكيلسين Albert Michelson) و(إيدوارد مورلي Edward Morley) اللي اتعملت عشان يعرفوا خواص الأثير Aether اللي هو المادة الأسطورية اللي كان بيتقال إن الضوء بينتقل من خلالها .. هم جابو مسطبة طوب وحطوا فيها حلة إتحط فيها زئبق وفوقيها لوح خشب عشان يركبوا عليه التجربة.

الناس وقتها كان مقتنعة بإن الضوء هو موجة برده زيه زي الصوت بس بينتقل من خلال حاجة إسمها الأثير .. الأثير ده يبقي حاجة إحنا مش عارفينها بس غالباً يعني الحاجة دي شفافة لإن إحنا مش بنشوفها .. حاجة كتير أوي لإنها حولينا في كل حتة .. حاجة غير قابلة للإنضغاط لإنك بتلاقيها في الغلاف الجوي للأرض وكمان في الفضاء الخارجي .. بإختصار الأثير ده كان الفنكوش .. ناس كتير كانت عارفة إنه فنكوش بس محدش عنده أي تفسير منطقي لإزاي الضوء بيتحرك فالمعترض علي فكرة الأثير ده مكنش قدامه حل غير إنه يحط جزمة في بقه ويسمع الكلام وهو ساكت لحد ما جه الثنائي (ألبيرت ميكيلسين) و(إيدوارد مورلي) .. الإتنين دول عملوا تجربة علمية عشان يدرسوا تأثير حركة الكرة الأرضية حول الشمس علي سرعة الضوء .. بإختصار شديد الناس أثبتت إن الأثير ده فنكوش .. مفيش حاجة إسمها أثير .. الضوء له سرعة ثابتة أيا كان هو ماشي فين وإمتي .. العالم فضل مصدوم مش عارف يرد لحد ما جت سنة 1905 لما (ألبيرت أينشتاين Albert Einstein) نشر الرسالة العلمية بتاعة النظرية النسبية الخاصة Special Relativity.

الشغل اللي عمله (أينشتاين) مهم أوي إنك تبقي فاهم إنه مجابوش من دماغه .. (أينشتاين) بني علي شغل التجربة بتاعة (ألبيرت ميكيلسين) و (إيدوارد مورلي) وكمان مبنية علي الشغل بتاع (بيرنارد ريمان) وعشان تفهم ده إنت محتاج تبص علي عنوان الرسالة بتاعة (أينشتاين) .. النسبية الخاصة:

هي إتسمت نسبية لإن النظرية رمت في الزبالة فكرة الأثير اللي هو كان الMedium أو الحاجة اللي الضوء بينتقل فيها .. ده معناه إن سرعة الضوء في الفراغ هي سرعة ثابتة .. ده معناه برده إن الزمن Time والفراغ أو المكان Space مش حاجتين منفصلين إنما هما حاجة واحدة إسمها الزمكان أو Space-time .. لحد هنا ده الجزء من شغل (أينشتاين) اللي إتبني علي تجربة (ألبيرت ميكيلسين) و(إيدوارد مورلي).
هي إتسمت خاصة لإن اللي بيقوله (اينشتاين) إن الزمكان أو Space-Time ده مش عبارة عن ورقة كراسة مستوية .. دي ورقة كراسة بس كيرفي .. زي ما إنت لما بتقطع ورقة كراسة وتمسكها من طرفها وتقف في البلكونة وتلاقي الورقة بتتمايل مع إتجاه الهواء فبرده الزمكان شكل الكيرف بتاعه بيتغير بس بناء علي تأثير الجاذبية .. وده الجزء من شغله اللي إتبني علي اللي قاله (بيرنارد ريمان).

ده معناه إيه في الأخر؟ .. معناه إن الكلام بتاع (إقليدس) والكلام بتاع (أينشتاين) هم بالضبط نفس الحاجة بس ده العامي وده الفصيح .. بص كده علي بيت الشعر ده .. أجارتنا أنا غريبان هاهنا .. وكل غريب للغريب نسيب .. ده بيت شعر كتبه (أمروء القيس) بيتغزل فيه في بنت جارته .. بص بقي الكوبليه ده من أغنية بنت الجيران بتاعة (حسن شاكوش) .. بنت الجيران شاغلالي أنا عيني .. وأنا في المكان في خلق حواليا .. في الحالتين بتتكلم عن رجل بيحب جارته بس في الحالة الأولانية هو بيتكلم بلغة فصحي في رأي ناس كتير إنها مجعلصة .. وفي الحالة الثانية إنت قدام لغة بسيطة يفهمها سواق التوكتوك وخريج الAUC .. كلام (إقليدس) هو النسخة المبسطة من الهندسة .. النسخة اللي فيها خطوط مستقيمة ومثلثات زواياها 180 درجة .. الهندسة الحقيقية هي هندسة الكيرفات .. هي هندسة (أينشتاين) .. هي هندسة (ياسمين الخطيب) .. هل معني كده إن (إقليدس) غلطان؟ .. بالتأكيد لا .. هو بس مكنش شايف الصورة كاملة .. زي اللي عارف يعني إيه كورة قدم من سماع الماتشات في الراديو.

المصادر: